How To Solve This Crazy Equation. Ramanujan's Radical Brain Teaser

Ramanujan Kökleri | Matematiksel

Ramanujan Kökleri | Matematiksel

ELİF ve VAV'ın HİKAYESİ

Matematik güzeldir

Matematik güzeldir (hayır, gerçekten)

Bazı matematiksel güzellik vakaları açıktır. Örneğin fraktallar , kendi kendine benzerliği çarpıcı ve sayısız sanatçıya ilham veren matematiksel sayı kümeleridir.

Az daha çoktur

Peki ya daha az belirgin vakalar? Sana bir örnek vermeye çalışayım. Belki 1, 3, 6, 10, 15, 21, 28,… sayıların sırasını tanıyorsunuzdur. Bu, öğrencilerin okulda sıkça karşılaştıkları bir dizidir: üçgen sayılar . Dizideki her sayı, bir üçgen dizisindeki noktaların sayısına karşılık gelir.

Altı ilk üçgen sayı: 1, 3, 6, 10, 15, 21.

Sıradaki 1000'inci sayı olacağını tahmin edebilir miyiz? Bu sorunun üstesinden gelmenin birçok yolu vardır ve aslında bu yaklaşımlar arasındaki benzerlik ve farklılıkları gidermek hem matematiksel hem de aydınlatıcıdır. Fakat burada oldukça güzel bir argüman var.

Sıradaki 10. sayıyı hayal edin (çünkü resmi çizmek 1000'inkinden daha kolay!). Noktaları saymadan noktaları sayalım. Noktalar üçgeni, alt satırda 10 ve 10 satır nokta var.

Bu düzenlemenin başka bir kopyasını çıkarırsak, onu döndürerek orijinal nokta üçgenimizin yanına koyabiliriz - böylece iki üçgen bir dikdörtgen oluşturur. Bu nokta şekli, alt satırda 10 ve 11 satır olacaktır, bu nedenle toplamda 10 x 11 = 110 nokta vardır (aşağıdaki resme bakın). Şimdi bunların yarısının orijinal üçgenin içinde olduğunu biliyoruz, bu yüzden 10. üçgen sayısı 110/2 = 55'tir. Onları saymak zorunda kalmadık.

10. üçgen sayı x2.

Bu matematiksel argümanın gücü, noktaları çizmeden bile, herhangi bir sayıya acısız şekilde genelleştirebilmemizdir. Düşünce deneyi yapabiliriz. Dizideki 1000. üçgen alt satırda 1000 noktaya ve 1000 nokta noktaya sahip olacaktır. Bunun başka bir kopyasını alarak ve döndürerek, alt satırda 1000 nokta ve 1001 satırdan oluşan bir dikdörtgen elde ederiz. Bu noktaların yarısı orijinal üçgendeydi, bu nedenle 1000'inci üçgen sayısı (1000 x 1001) / 2 = 500500'dü.

Benim için nokta çizme, çoğaltma, döndürme ve dikdörtgeni yapma fikri çok güzel. Argüman güçlüdür, düzgün bir şekilde genelleştirir (üçgenin herhangi bir boyutuna) ve cevabın neden ne olduğunu açıklar .

Bu sayıyı tahmin etmenin başka yolları da var. Birincisi, dizinin ilk birkaç terimine bakmak, bir formül tahmin etmek ve ardından formülün işe yaradığını ispatlamaktır (örneğin , indüksiyonla ispat denilen bir teknik kullanarak ). Ancak bu, aynı unutulmaz açıklamayı formülün arkasına taşımaz. Nokta resimleriyle tartışılan bir ekonomi var, tek bir diyagram bilmemiz gereken her şeyi yakalar.

İşte çekici bulduğum başka bir argüman. Aşağıdaki toplamı düşünelim:

Harmonik seri

Bu ünlü harmonik dizisidir . Sonlu bir sayıya eşit olmadığı ortaya çıkıyor - matematikçiler toplamın "farklılaştığını" söylüyorlar. Bunu nasıl kanıtlayabiliriz? Kulağa zor geliyor, ancak zarif bir fikir işi yapıyor.

Gruplandırılmış terimlerle harmonik seriler.

Burada her kesir grubu ½'dan daha fazla ekler. ⅓'nın than'dan daha büyük olduğunu biliyoruz. Bunun anlamı (⅓) + (¼), ¼'ye eşit olan (¼) + (¼) değerinden daha büyüktür. Böylece, her biri than'den büyük olan yeterli blok ekleyerek, toplam büyür ve büyür - istediğimiz hedefi yenebiliriz. Sonsuz sayıda ekleyerek sonsuz miktarda alacağız. Sonsuzluğu güzelleştirdik, güzel bir argümanla.

Bekleme oyunu?

Bunlar matematiğin en zor parçaları değil. Matematiğin zorluklarından biri, daha sofistike problemlerle uğraşmanın genellikle daha sofistike terminoloji ve notalarla uğraşmak anlamına gelmesidir. Önce doğru bir şekilde anlamadığım sürece güzel bir matematik parçası bulamıyorum - ve bu estetik nitelikleri takdir etmem biraz zaman alabilir anlamına geliyor.

Bunun matematiğe özgü olduğunu sanmıyorum. İlk başta onların güzelliğini veya zerafetini anlamadığım müzik parçaları, binalar, görsel sanat eserleri var - ve sadece fikirlerle boğuşarak, güzelliği algılamaya geldiğim için ısrar ederek.

Benim için, lisans öğretmeni sevinçlerinden biri, matematiğin güzelliği ile ilgili kendi takdirlerini geliştirmelerini izlemektir. İkinci öğleden sonralarımı ev ödevlerini gözden geçirmek için göreceğim ve farklı çözümler hakkında ilginç bir sohbete başlayacağımızı biliyorum - ve estetik nitelikleri göz önünde bulundurmanın anlayışlarını derinleştirmede rol oynayacağını çoktan biliyorum Matematiğin

Okul öğrencileri de aynı deneyime sahip olabilir: Zengin sorularla meşgul olma fırsatı verildiğinde, matematiksel fikirlerle oynayabildikleri zaman, aynı soruya birden fazla strateji deneyimleme şansı buldukları zaman ders kitabının arkası ve devam ediyor. Matematiksel fikirler üniversite düzeyinde olmak zorunda değildir, okul öğrencileri için mükemmel olan güzel problemler vardır . Ne mutlu ki, birçok matematik öğretmen ve güzelliği bu deneyimlere sahip öğrencilerin yardımcı olan matematik eğitim projeleri vardır 

.Matematik güzeldir ------------------------------------------------

Mathematics is beautiful (no, really)

Fractals in stone by Jami Masjid.
Ankush.sabharwal/wikipedia, CC BY-SA

Vicky Neale, University of Oxford



For many people, memories of maths lessons at school are anything but pretty. Yet “beautiful” is a word that I and other mathematicians often use to describe our subject. How on earth can maths be beautiful – and does it matter?

For me, as a mathematician, it is hugely important. My enjoyment of the beauty of mathematics is part of what motivates me to study the subject. It is also a guide when I am working on a problem: if I think of a few strategies, I will choose the one that seems most elegant first. And if my solution seems clumsy then I will revisit it to try to make it more attractive.

I’ve just finished marking a pile of homework from my second-year mathematics undergraduates. I am struck by two students’ contrasting solutions to one problem. Both solutions are correct, both answer the question. And yet I much prefer one to the other. It’s not just that one is longer than the other, or that one is explained better than the other (both are described well, in fact).

The longer one doesn’t quite get to the heart of the matter, it’s a bit cluttered with unnecessary distractions. The other uses a different approach, which captures the essence of the ideas – it helps the reader to understand why this piece of mathematics works this way, not just that it does. For a mathematician, the “why” is critical, and we are always looking for arguments that reveal this.

Some cases of mathematical beauty are clear. Fractals, for example, are mathematical sets of numbers – corresponding to shapes – that have striking self-similarity and that have inspired numerous artists.

Less is more

But what about less obvious cases? Let me try to give you an example. Perhaps you recognise the sequence of numbers 1, 3, 6, 10, 15, 21, 28, … This is a sequence that students often encounter at school: the triangular numbers. Each number in the sequence corresponds to the number of dots in a sequence of triangles.

The six first triangular numbers: 1, 3, 6, 10, 15, 21.

Can we predict what the 1000th number in the sequence will be? There are many ways to tackle this question, and in fact unpicking the similarities and differences between these approaches is in itself both mathematical and enlightening. But here is one rather beautiful argument.

Imagine the 10th number in the sequence (because it’s easier to draw the picture than for the 1000th!). Let’s count the dots without counting the dots. We have a triangle of dots, with 10 in the bottom row and 10 rows of dots.

If we make another copy of that arrangement, we can rotate it and put it next to our original triangle of dots – so that the two triangles form a rectangle. This shape of dots will have 10 in the bottom row and 11 rows, so there are 10 x 11 = 110 dots in total (see figure below). Now we know that half of those were in our original triangle, so the 10th triangular number is 110/2 = 55. And we didn’t have to count them.

The 10th triangular number x2.

The power of this mathematical argument is that we can painlessly generalise to any number – even without drawing the dots. We can do a thought experiment. The 1000th triangle in the sequence will have 1000 dots in the bottom row, and 1000 rows of dots. By making another copy of this and rotating it, we get a rectangle with 1000 dots in the bottom row and 1001 rows. Half of those dots were in the original triangle, so the 1000th triangular number is (1000 x 1001)/2 = 500500.

For me, this idea of drawing the dots, duplicating, rotating and making a rectangle is beautiful. The argument is powerful, it generalises neatly (to any size of triangle), and it reveals why the answer is what it is.

There are other ways to predict this number. One is to look at the first few terms of the sequence, guess a formula, and then prove that the formula does work (for example by using a technique called proof by induction). But that doesn’t convey the same memorable explanation behind the formula. There is an economy to the argument with pictures of dots, a single diagram captures everything we need to know.

Here’s another argument that I find attractive. Let’s think about the sum below:

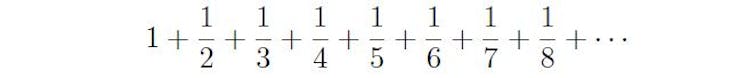
The harmonic series.

This is the famous harmonic series. It turns out that it doesn’t equal a finite number – mathematicians say that the sum “diverges”. How can we prove that? It sounds difficult, but one elegant idea does the job.

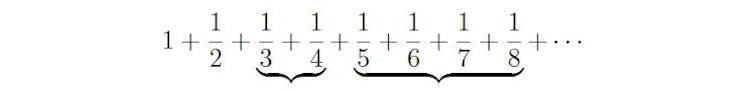
The harmonic series with grouped terms.

Here each group of fractions adds up to more than ½. We know that ⅓ is bigger than ¼. That means (⅓) + (¼) is bigger than (¼) + (¼), which equals ½. So by adding enough blocks, each bigger than ½, the sum gets bigger and bigger – we can beat any target we like. By adding an infinite number of them we will get an infinite sum. We have tamed the infinite, with a beautiful argument.

A waiting game?

These are not the most difficult pieces of mathematics. One of the challenges of mathematics is that tackling more sophisticated problems often means first tackling more sophisticated terminology and notation. I cannot find a piece of mathematics beautiful unless I first understand it properly – and that means it can take a while for me to appreciate the aesthetic qualities.

Can you appreciate the beauty of Kazimir Malevich’s ‘Black Square’?
wikipedia

I don’t think this unique to mathematics. There are pieces of music, buildings, pieces of visual art where I have not at first appreciated their beauty or elegance – and it is only by persevering, by grappling with the ideas, that I have come to perceive the beauty.

For me, one of the joys of teaching undergraduates is watching them develop their own appreciation of the beauty of mathematics. I’m going to see my second years this afternoon to go over their homework, and I already know that we’re going to have an interesting conversation about their different solutions – and that considering the aesthetic qualities will play a part in deepening their understanding of the mathematics.

School students can have just the same experience: when they’re given the opportunity to engage with rich questions, when they can play with mathematical ideas, when they have the chance to experience multiple strategies to the same question rather than just getting the answer in the back of the textbook and moving on. The mathematical ideas do not have to be university level, there are beautiful problems that are perfect for school students. Happily, there are many maths teachers and maths education projects that are helping students to have those experiences of the beauty of mathematics.

Vicky Neale, Whitehead Lecturer at the Mathematical Institute and Supernumerary Fellow at Balliol College, University of Oxford

This article is republished from The Conversation under a Creative Commons license. Read the original article.